Je confirme ce qui est dit au dessus. Aussi bizarre que cela paraisse on indique une CMU en industrie (Charge Maximale d’Utilisation) qui inclue par exemple pour du levage un facteur de sécurité de 4, tandis qu’en escalade c’est la charge à rupture qui est indiquée.
Ce qui est sous-jacent c’est qu’un mousqueton d’escalade ayant été soumis à une forte charge néanmoins inférieure de la valeur indiquée pourra nécessiter une mise au rebut pour cause de déformation permanente.
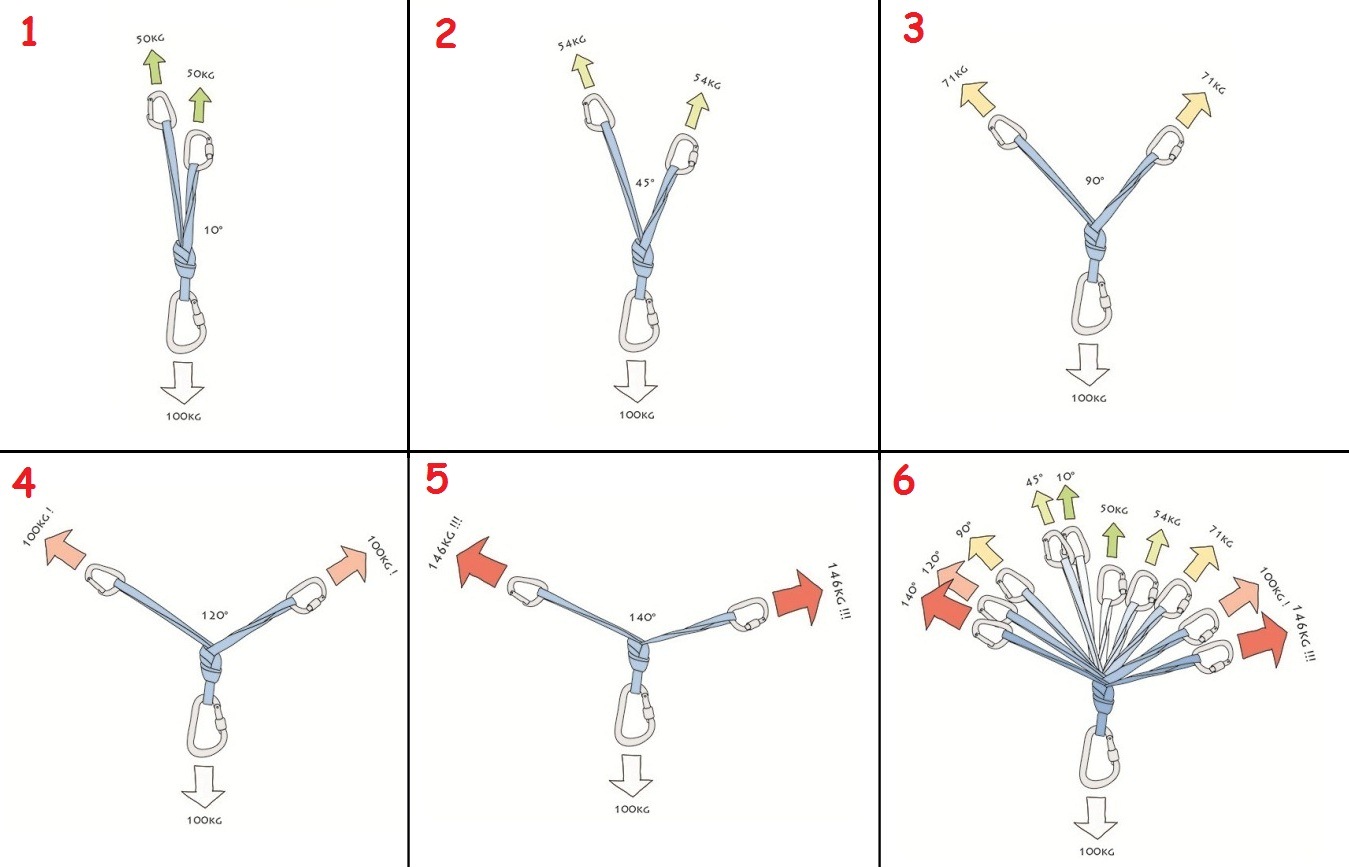
Triangulation
Quand j’ai dit ça, je pensai à « un mousqueton résiste a 2200daN, pas 2200 Kg » pck un mousqueton ne peut pas résister à une masse, un mousqueton résiste a une force !! même si je sais bien que lorsque l’on dit 2200kg , on parle de kg statique ou de kgF.
Pour les autres :
En escalade, la valeur indiqué par le fabriquant correspond à « le fabricant garanti que le mousqueton peut supporter une force de 22kN ».
Par contre, en industrie (maillon rapide, etc), le matériel est donné avec une CMU (charge maximale d’utilisation) et une CDR (charge de rupture).
Le coefficient de sécurité dépend de l’EPI (corde/mousqueton/poulies/etc…) et est calculé à partir de la CDR.
http://www.auvieuxcampeur.fr/14-mm-goliath.html
enfin tout ça, c’est en théorie … : http://www.expe.fr/fr/corde-access-10-5-mm-unicore.html
Dans tout les cas, le vendeur est censé préciser si la résistance qu’il donne est la CMU ou CDR .
Le professionnels est censé connaitre les coefs de secu en fonction du matos, et peut donc calculer l’un ou l’autre en fonction de ce qu’il a
Non, c’est le contraire : le fabricant garantit que le mousqueton ne casse pas en dessous de 2200daN. Mais il ne garantit rien au-dessus. En réalité, il peut casser à 2500daN, tu ne pourras rien repprocher au fabricant 
Oui, en effet, je me suis embrouiller dans mes implications 
rebéotien : quand les deux points sont à peine alignés dans l’axe vertical, en plus de visu très difficile d’équilibrer les forces : ça ne tient pas ! :o quid des relais avec une corde molle qui relie les deux points, même plus ou moins dans l’axe vertical ?
oui, bien sur ce n’est plus de la triangulation, mais justement…
En y réfléchissant, quand tu veux relier 2 point alignés à la verticale, tu devra ajuster le plus possible les longueurs de tes sangles, sinon tout le poids du grimpeur sera sur 1 point. Alors que lorsque ils sont alignés sur le plan horizontal, on n’est pas à 1 ou 2 cm de sangle.
Mais en pratique, le nœud sera plus tendu sur le point qui travaille, et essayera de valoriser le plus possible l’autre point, bien que le plus souvent, il ne servira presque à rien.
Sauf si le point qui travaille casse, a ce moment la, c’est le point d’en dessous qui récupérera la charge, et, il te faudra donc ajuster ta sangle au mieux afin de minimiser le choque de reprise.
Rebonjour a tous !
J’ai enfin trouver une formule qui permet de trouver les valeur en fonction des angles autrement que par un dessin !
En effet, jusqu’ici, je contournai le probleme par une résolution graphique, ce qui me limitait a utiliser geogebra, mais maintenant,
je vais essayer de coder un programme en java, et donc, exécutable sous android,
cela sera sans doute moins pratique (on entre les 2 angles au lieu de faire bouger les points ou curseurs)
mais il suffira d’emmener un téléphone sous android pour calculer les rapports de force !
Et pour ceux que cela intéresse, voici les formules accompagné d’un schéma :

N’hésitez pas si vous avez des questions !
edit : les formules ont été modifiées, elles sont maintenant exactes, merci à xabier 
Tes formules ne sont pas cohérentes avec tes graphiques geogebra,… 
ah oui, effectivement, j’ai inversé f1 et f2 :s
je modifie ça le plus tôt possible
edit : fait ! encore merci !
de rien 
Si tu veux encore simplifier tes expressions et les rendre plus « belles » tu peux utiliser les identités:
sin(180-a) = sin(a)
et
sin(2a) = 2*sin(a)*cos(a)