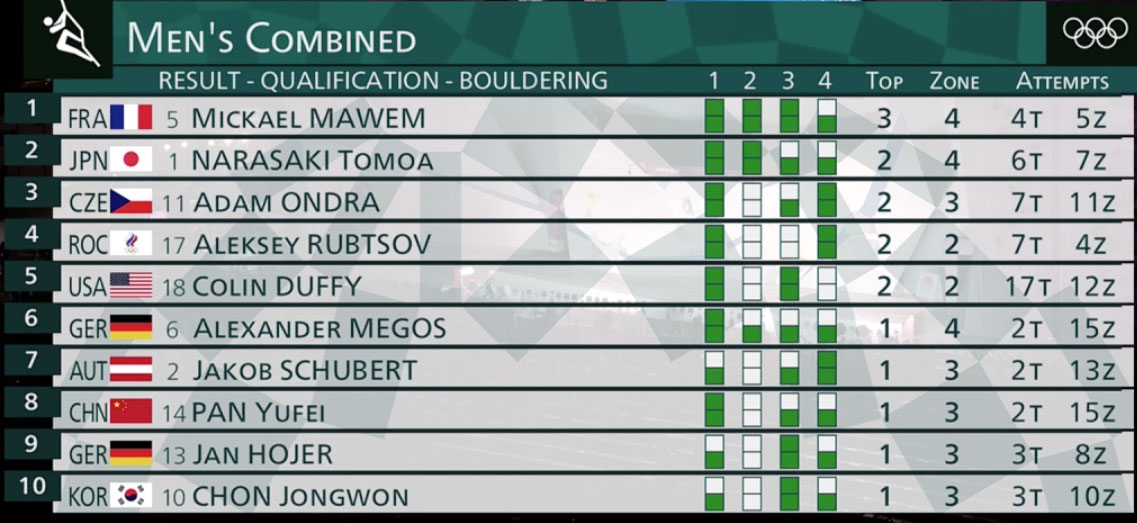
Adam 3éme provisoire sur 14 passés
JO Tokyo 2021
merci, malheureusement je ne peux pas le voir depuis ma zone geographique (US) …
2 français en finale, si je comprends le principe du truc
Le seul moyen est de passer par le site de NBC si tu as un abonnement TV. Sinon c’est bien verrouillé cette année.
pas de TV malheuruesement (ou heureusement en general!)
Pareil et on s’en passe bien.
Tu peux essayer peackock. Je n’ai pas osé.
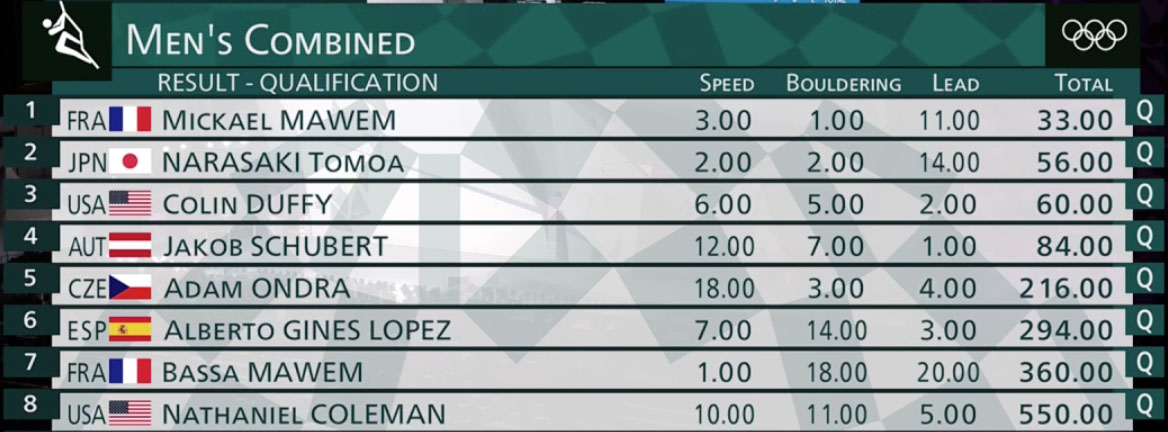
En jouant la finale avec les résultats actuel: les 1,2,3,4,5,6,7,8 arrivent respectivement 1,2,3,4,6,7,5,8
PS: je répondais à personne.
J’ai l’impression qu’un des frangins s’est fait bien mal, du coup forfait pour la finale et repêchage de Megos?
Merci pour le calcul, du coup c’est si bidon que ca en a l’air cette histoire de multiplication 
Et si vous préférez les additions et prendre le plus grand score que multiplier et prendre le plus bas, pour une finale à 8 le système est équivalent à ramasser en fonction du classement :
1: 123 points, 2: 82 points, 3: 58 points, 4: 41 points, 5: 28 points, 6: 17 points, 7: 8 points, 8: 0 points
Et à additionner les trois scores, le plus grand gagne.
(la multiplication fait juste une pondération en prenant le log de chaque classement, parce que le log est strictement croissant donc conserve le classement et que log(a*b*c)=log(a)+log(b)+log(c). Et j’ai fait un bout de code pour trouver les plus petites valeurs entières qui donnent les bons résultats pour 8 personnes.)
Merci pour le calcul et l’exemple.
Comment a tu trouvé tes valeurs ? Je n’ai pas suivi. Une solution pour éviter les doublons ?
en finale comment il départage 1x1x8 et 2x2x2 par exemple ?
Bonjour à tous. Quelqu’un a le tableau des résultats?
Je suppose que les compteurs repartent à zéro pour la finale, du coup la contre perf de Ondra en diff n’a pas d’incidence par exemple?
[disgression maths]
Pour détailler un peu plus:
-
Comme le logarithme conserve l’ordre, classer les gens dont les rangs sont a,b,c par a*b*c revient au même que les classer par log(a*b*c)
-
Le logarithme a la propriété que log(a*b*c)=log(a)+log(b)+log(c)
-
Donc on pourrait dire que dans chaque épreuve si on a le rang a on gagne log(a) points, et qu’il faut le minimum de points au total
-
Pour que ce soit le maximum, on peut tout multiplier par -1 et dire qu’on gagne -log(a) points
-
Si on ajoute une constante et qu’on multiplie par une constante positive chaque score, ça ne change pas le classement ce qui permet :
- Pour que les scores soient positifs et le dernier à zéro, on peut prendre log(8)-log(a)
- Enfin on peut multiplier ça pour que ça tombe « à peu près » sur des entiers, et vérifier que si on arrondit à l’entier ça ne change pas les classements pour tous les résultats possibles, ce que j’ai automatisé avec un petit programme. D’où les valeurs trouvées.
[/maths]
Y’a aussi les résultats complets et détaillés sur le site de l’IFSC (entre autres).
Pas tout compris mais je trouve que ça pénalise le 3ème Colin Duffy qui a pourtant été le plus régulier.
Tout à fait.