Salut à tous,
je cherche un prof de méca pour m’adapter ce schéma:
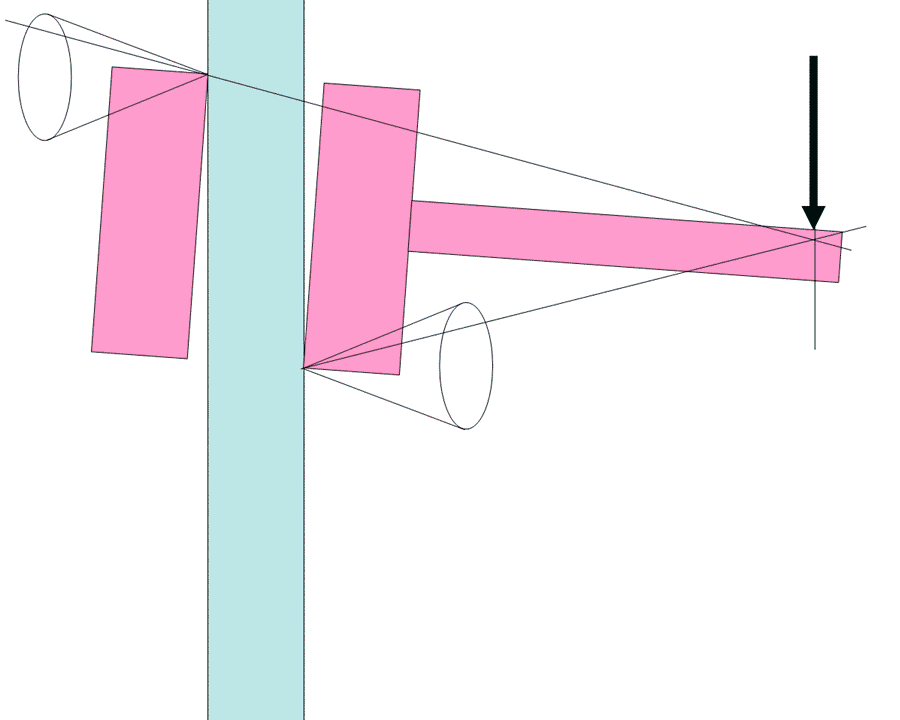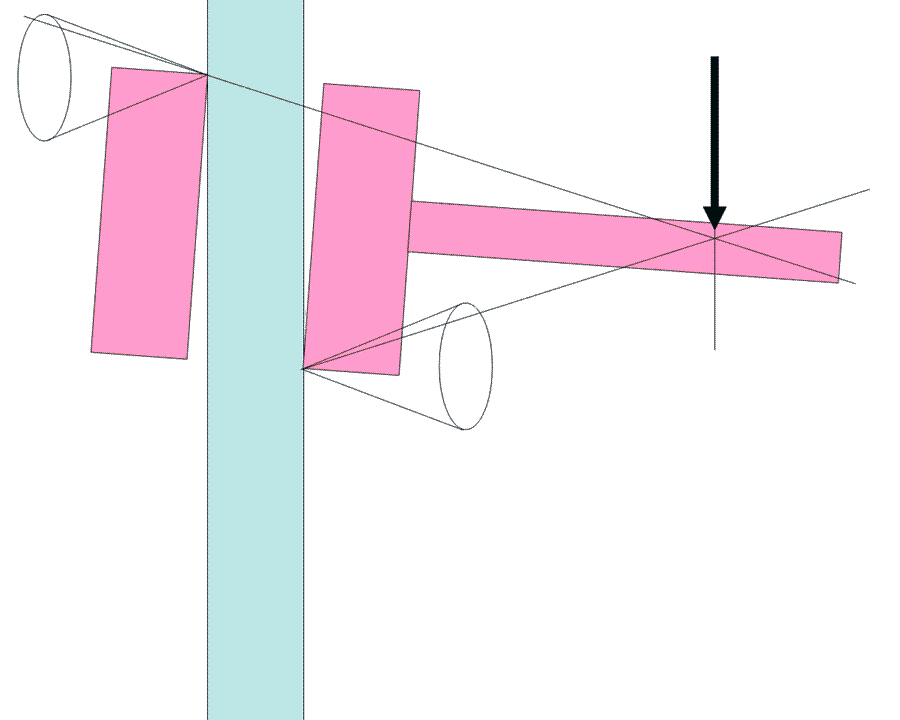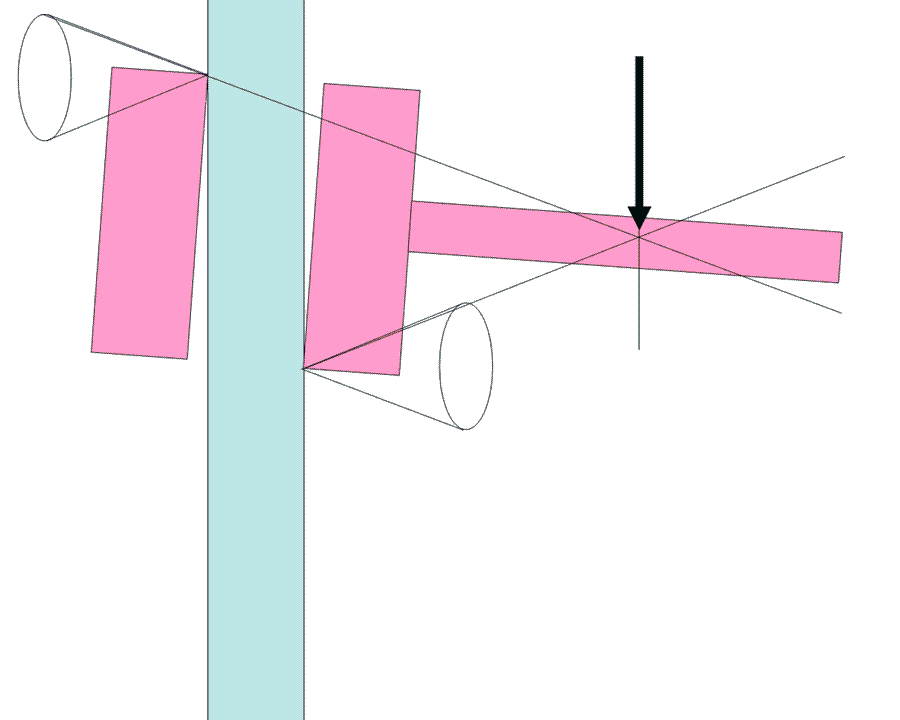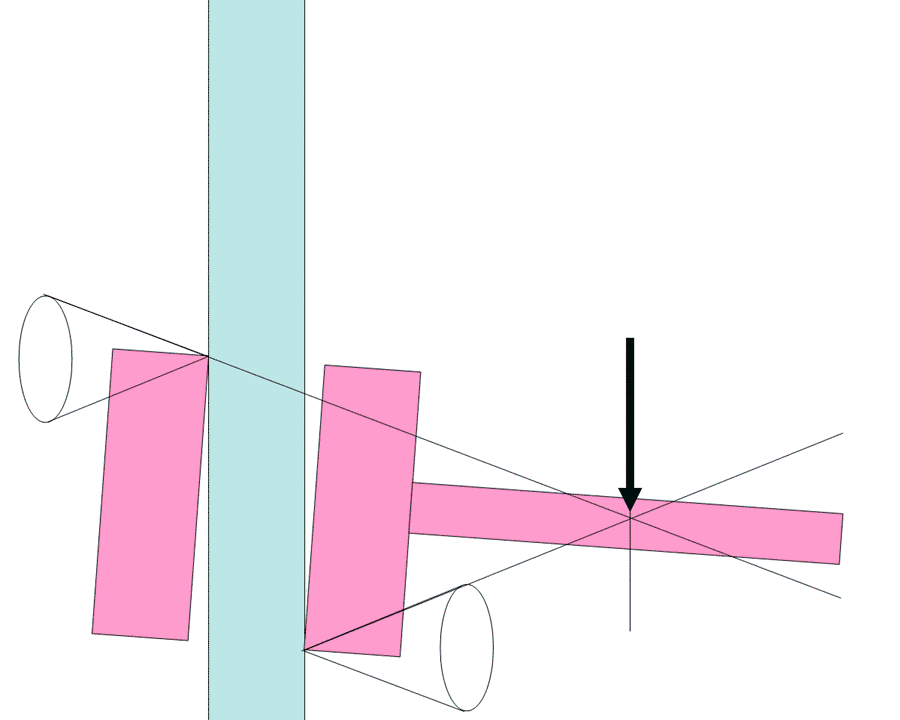
au cas d’un piton. C’est à dire: rocher en rouge, Piton en bleu. Force sur le piton , bien sûr.
Merci
Étude mécanique des pitons
Le piton travaille comment ?
- Piton dans une fissure horizontale, et force appliquée sur l’oeil du piton, dans un plan vertical. En faisant varier l’angle de la force, on reproduit la variation de la force aux points de contact piton/rocher du schéma ci-dessus (quand la composante axiale dépasse le frottement, le piton glisse).
- Piton dans une fissure verticale, et oeil décalé. Une force verticale sur l’oeil crée un porte à faux et fait mordre le piton. Ce n’est pas vraiment pareil que le cas précédent, car ici le piton peut tenir une forte charge car il creuse une rainure dans le rocher, ce n’est pas du simple frottement.
Tu veux illustrer le phénomène d’arc-boutement dans le cas d’u piton dans fissure c’est ça ?
Pour bien modéliser il faut préciser quel cas de charge tu veux traduire (cf message bubu).
Merci pour vos réponses. J’arrive à illustré l’arc-boutement d’un Friend ( avec les cônes d’adhérence et la projection de la force de contact…) mais je n’arrive pas à faire la même chose dans le cas d’un piton ( fissure horizontale: cas le plus simple) . Je ne comprend pas quand ma force va sortir des cônes.
Pas certain d’avoir compris ce que tu voulais faire mais je tente :
Dans le cas d’un piton dans une fissure horizontale avec un piton qui serait uniquement en contact en 2 points opposés, et que tu le charges dans son axe (Fx=0) verticalement, tu seras toujours dans le cône de frottement et tu auras toujours adhérence même avec un coeff frottement nul donc comme tu le dis elle ne sort pas du cone de frottement. Si tu ajoutes une composantes axiale (Fx différent de zero) au piton dans ce cas le coef de frottement intervient mais ce n’est pas de l’arc boutement et il y a un risque de glissement si Fx augmente.
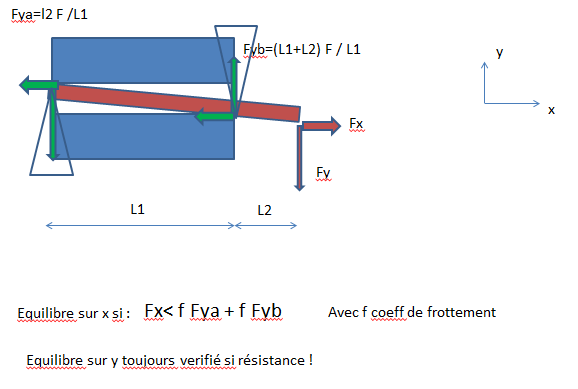
Tu peux nous la refaire avec un piton mi-dur ?
Avec Abaqus et si tu me donnes la loi de comportement, pas de pb -))
Je t’avoue que j’ai hésité à répondre parce qu’on sait jamais ce qu’attend l’interlocuteur…
Et je te signale que tu n’as pas fini de saisir ta sortie à la Meije !
Merci pour les explications et le temps passé pour faire le schéma.
Donc si ce n’st pas de l’arc-boutement est ce pour autant de l’adhérence ? Ou il y-a-t-il autre chose ?
Encore merci.
J’ai pas fini la sortie !
Non je rigole, mais c’est presque ça !
C’est très compliqué un piton et pas qu’en raison de l’inhomogénéité du support. Le piton travaille en adhérence élastique avec une torsion (oeil décalé de l’axe, acier dur) :
ou même plus caractéristique sur l’adhérence crée par déformation élastique :

ou en blocage mécanique après déformation plastique pour un piton en acier mi-dur avec oeil centré : typiquement l’universel

Et tous les cas entre les deux extrêmes comme toujours !
Intéressé par la tenue par adhérence ( une chose après l’autre, les déformations, effet de levier, torsions… seront pour plus tard) je veux bien être instruit sur:
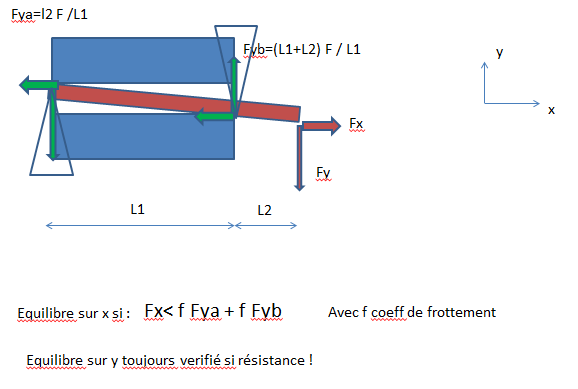
ce cas avec Fx supérieure à FY.
Et sur le concept adhérence élastique de Gros.
merci
En fait, il faut lire frottements liés aux efforts de déformations élastiques du piton dans la fissure.
Bon, donc vous n’auriez pas une réponse claire sur la tenue des pitons ( comme des cablés ) par arc-boutement , situation similaire au tiroir qui se coince lorsqu’on cherche à le sortir ?
Quand l’effort est dans un plan vertical, un piton travaille en arc-boutement uniquement si la fissure n’est pas horizontale.
En gros, il faut que la force sur l’oeil du piton ne soit pas dans un plan perpendiculaire à la fissure.
Dans le cas d’une fissure horizontale, le piton tient par coincement : frottement par la déformation élastique du piton (sur son épaisseur) et du rocher, et dont la limite de glissement est indépendante de l’effort sur l’oeil.
Dans le cas d’un arc boutement, la limite de glissement dépend de l’effort sur l’oeil, et le but est qu’elle soit proportionnelle pour que ça tienne toujours quel que soit l’effort (tant que le rocher ou le piton ne se déforme ou ne s’érode pas trop).
Réponse tardive à cause de grimpe…
Je tente à nouveau…mais comme je ne sais pas trop d’où je dois partir et où je dois arriver pour répondre à tes questions, les puristes pourront critiquer et les autres pourront dire que c’est de l’enc… de mouche, mais on est sur C2C -)
préambule que tu peux sauter si tu connais déjà :
Pour être d’accord sur le termes justes quelques définitions pour que l’on soit d’accord de quoi on parle.
Le frottement c’est le phénomène et il peut y avoir 2 cas : glissement ( il y a mouvement entre les solides en contact) ou adhérence (pas de mouvement). Si tu pousses une caisse sur le sol en augmentant progressivement ton effort au début tu as de l’adhérence puis (si la caisse ne bascule pas avant , je sentais venir la remarque des puristes) puis elle se mettra à glisser. Le modèle le plus simple pour traduire les phénomènes de frottement et le modèle de coulomb (ce modèle est très imparfait, tout le monde le sait mais sinon cela de vient vite plus compliqué). Globalement il dit que la composante de frottement est tangentielle au contact et de sens opposé au mouvement (réel ou supposé). Tant que le rapport composante normale sur composante tangentielle (due au frottement) est inférieur au coefficient de frottement f (qui dépend essentiellement des 2 matériaux en contact) on a adhérence, sinon il il y a glissement. Graphiquement cela peut se traduire par un cône de frottement (un triangle dans le plan), si la composante tangentielle fait que l’on est dans le cône on aura adhérence, si on est pile sur la surface on est à limite du glissement mais si pour avoir équilibre il faut que la composante de frottement sorte du cône et c’est impossible donc tu auras glissement. Tu peux quantifier le demi angle au sommet de ce cône par alpha=atan f . un coeffcient de frottement de 0,2 signifie que la composante tangentielle ne peut pas être supèrieure à 0,2 la composante normale et cela correspond à un demi angle au sommet de 11,3°.
Revenons au tiroir de notre grand mère,…ou à notre coinceur.
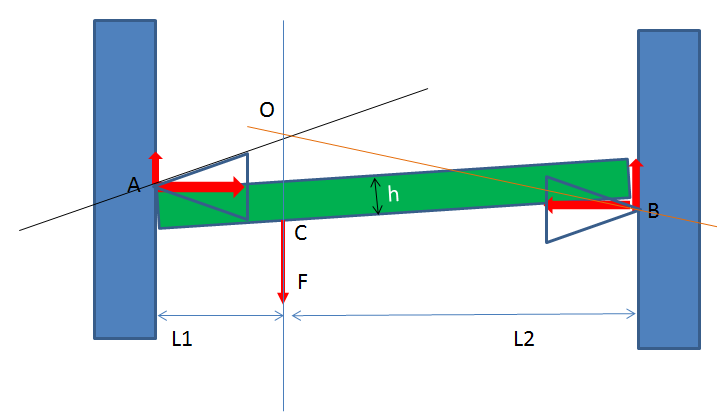
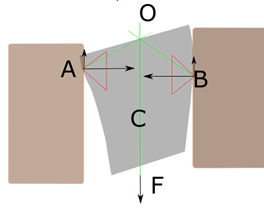
Je te propose le schéma ci dessous . Une fissure verticale (en bleu), le tiroir (en vert). quand on tire en avec une force en C il se met en travers et vient en contact en A et B.
Imaginons le cas ou en A on soit à la limite du glissement (en fait on est obligé de faire une hypothèse pour résoudre complétement). A la limite du glissement les composantes en A seront donc orienté suivant la droite noire. Pour avoir équilibre il faut (entre autre) que les droites support des 3 actions A,B,C soit concourrantes en un point O. Le point O est défini par l’action en A (noire) et C (bleue), on peut donc tracer la droite issue de B (marron). Si cette droite est à l’intérieure du cone en B il y aura équilibre sinon glissement.
Tu remarques que l’équilibre ne dépend pas de l’intensité de l’action F, mais que de sa position, cela veut dire que l’on peut avoir équilibre quelque soit l’intensité ça coince c’est la définition de l’arc boutement : équilibre quelque soit l’intensité. Si tu augmentes F les composantes tangentielles en A et B augmenteront proportionnellement mais leur direction ne changeront pas. Tu observes aussi les facteurs influents, si tu déplaces F vers la droite tu vois que l’action en B va se rapprocher du cône de frottement et là c’est le drame pour le grimpeur ou l’extase pour le tiroir de la grand mère ;-). L’autre paramètre influent est la hauteur h, plus il sera important plus il y aura glissement l’action en B (droite marron) marron se rapproche de l’extrémité du cône (Les tiroirs de nos grands mères sont larges et peu profonds h plutôt petit par rapport à la largeur L1+L2).
Si tu traces tout cela à l’échelle avec une valeur cohérente (que tu peux déduire des formes de tes friends favoris…) du coefficient de frottement (donc du cone) tu peux le résoudre graphiquement…
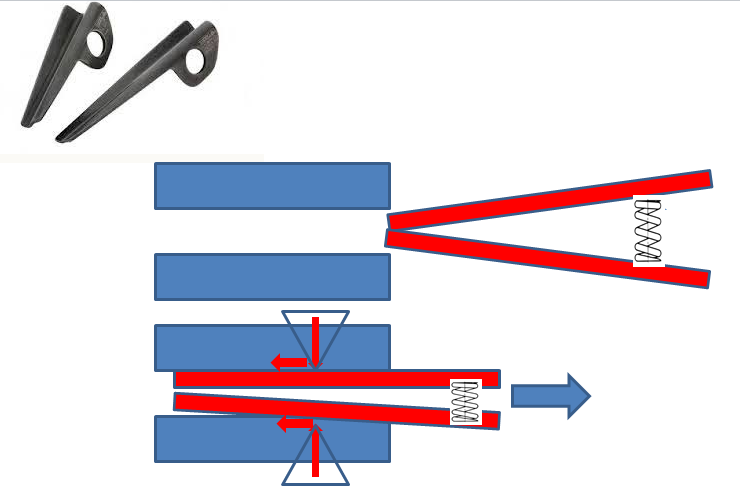
Passons au piton :
Il se comporte plutôt comme un composant élastique que j’ai symbolisé ci dessous à l’état libre puis à l’état déformé. Le fait de rentrer le piton, le déforme élastiquement (comprime le ressort pour symboliser). Du coup les composantes normales vont augmenter et si il y a frottement les composantes tangentielles aussi. Si tu veux sortir le piton il te faudra une force supérieure à ces composantes. Mais si tu bourrines comme @Gros tu y arriveras à passer d’adhérence à glissement, Cela dépend de l’intensité que tu mets ce n’est donc pas de l’arc boutement…
Super sympa de paser du temps pour me répondre. Là je n’ai pas le temps de digerer ton texte. Mais je fais ça dans les jours qui suivent. Merci!
c’est vraiment top de lire ces échanges sur c2c !!
Encore merci pour ton cours…
Mes souvenirs de méca sont lointains et je n’ai pas trace d’avoir abordé ces problèmes.
Donc si je résume à ma façon:
Dans le cas d’un coinceur de type câblé tant que le point d’application de la force F en O sera coïncidant avec la projection des forces résultantes en contact en A et B et dont les projections (AO et BO) seront dans le cône d’adhérence ; il y aura coincement par arc-boutement de la tête du coinceur . La valeur de la force F n’intervient pas dans un système par arc-boutement.
Questions:
-Tu fait remarquer que plus la distance verticale ( H sur ton schéma) entre A et B est faible, plus l’arc-boutement est facile à obtenir. Peut on en conclure qu’un coinceur à tête « courte » est plus efficace.
- Tu as tracé les distance L1 et L2 sur ton schéma mais sans les utiliser dans ton explication. Ont-elles un rôle ?
C’est sympa d’avoir des interlocuteurs capables de répondre à mes questions " existentielles " sur le matos!
le cas ecole pour le coinceur, c’est avec trois point d’appuis, bien isostatique
Comme tu l’as compris, plus que la hauteur totale du coinceur ce sont les points de contact qui sont importants, plus ils seront en vis à vis plus le coincement sera facile. Mais il y a aussi un incovénient que tu connais très bien (moi je suis plus un grimpeur de P1  ) c’est que les composantes normales (horizontales dans ton cas) seront très importantes en cas de chutes (F très grand), et donc si tu poses ton friend derrière une écailles fine, ben ça coince mais tu peux casser l’écaille…
) c’est que les composantes normales (horizontales dans ton cas) seront très importantes en cas de chutes (F très grand), et donc si tu poses ton friend derrière une écailles fine, ben ça coince mais tu peux casser l’écaille…
J’avais paramétré L1 et L2 pour montrer l’influence de la position de F (Non centrée par exemple) car je voulais proposer une résolution analytique (en écrivant les équations de la statique), mais au final il me semblait que la résolution (ou la visualisation graphique) était plus adaptée pour faire sentir les choses. L’intérêt est que tu peux facilement avoir une idée des intensités des efforts avec une chute facteur 2 par exemple…
Pas de pbs, pour info j’avais monté avec un collègue à l’université de grenoble une UE « Mécanique et Escalade ». C’était une UE transversale qui était proposée à des étudiants de sciences et de sport (beaucoup de grimpeurs dans le lot) , c’était sympa on résolvait des pbs de méca liés à l’escalade : effort lors des chutes, frottement et gestion du tirage, moufflage, themodynamique du descendeur,rdm des mousquetons, justification forme des firends…on faisait même un peu d’expérimental en salle…Bon on ne traitait pas la théorie des noeuds (un monde passionnant). Cette UE est passée à la trappe, c’est dommage on s’amusait bien !!
En fait le principal problème c’est la finesse de la modélisation, car les pbs rééls sont finalement assez complexe.
J’avoue que je ne comprends pas ta remarque. En fait dans tous les schémas qui ont été proposés on a fait l’hypothèse de pb plan, et même avec uniquement 2 points de contacts le pb est déjà hyperstatique, comme il y a du frottement aux contacts on se retrouve avec 4 inconnues pour 3 équations tu es obligé de faire une hypothèse pour résoudre complètement.
