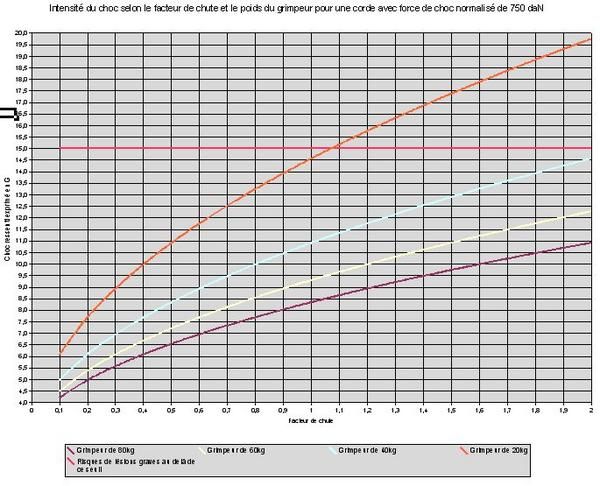
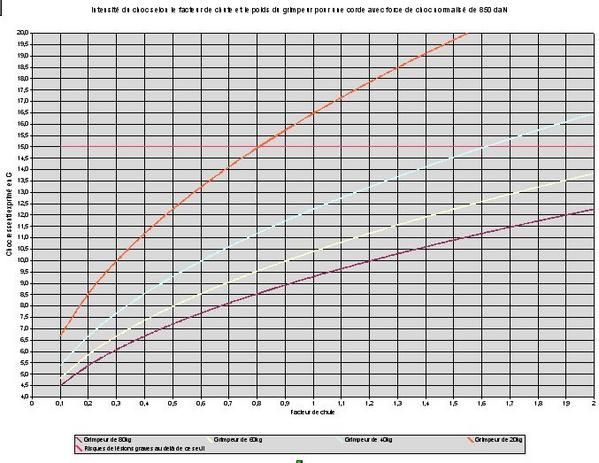
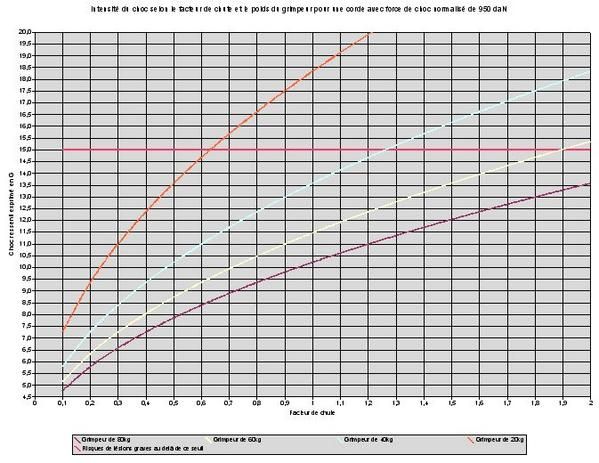
Posté en tant qu’invité par J2LH:
Gepi a écrit:
La décélération commence en même temps pour les 2, au moment où
la corde est tendue.
Pas tout à fait, la décélération commence au moment ou la force exercée par la corde est supérieur au poids, quand le poids du grimpeur est supérieure la décélération commence plus tard.
Posté en tant qu’invité par J2LH:
Gepi a écrit:
Non, l’approche intuitive conduit parfois à l’erreur.
Ca explique bien des idées reçues dans le domaine.
Posté en tant qu’invité par Gépi:
J2LH a écrit:
Pas tout à fait, la décélération commence au moment ou la force
exercée par la corde est supérieur au poids, quand le poids du
grimpeur est supérieure la décélération commence plus tard.
Tout à fait, je me demandais qui allait le relever en plus d’autres petits abus de ma part (il y en a d’autres) 
Posté en tant qu’invité par Pat:
merci pour tout Gepi.
Vas tu peaufiner le travail et resumer tout cela?
Ca serait domage que tout ces efforts soient perdus.
Et pour la difference de poids… avec tes formules, ca donne quoi?
Bravo aux autres aussi
Posté en tant qu’invité par Gepi:
Pat a écrit:
Et pour la difference de poids… avec tes formules, ca donne
quoi?
Avant de partir grimper (bonne soirée) :
C’est comme pour le temps de refroidissement du fût du canon.
« Un certain temps »
En fait c’est beaucoup trop variable d’une corde à l’autre (diamètre, peluchée ou pas, traitée dry ou pas, élasticité ,…)
Pour la variation du choc ressenti des graphiques me semblent plus parlant.
3 graphiques avec 3 cordes de forces de choc différentes, grimpeurs de 20, 40, 60 et 80 kg. Elles représentent le choc ressenti selon le facteur de chute en utilisant les données de Béal :
[%sig%]
Posté en tant qu’invité par J2MHV:
jon a écrit:
existe-t-il une medode de calcul pour determiner la difference
de poids maximum
possible entre l’assureur et le grimpeur (en tete et en moul)
dans le cas d’un site
de couennes ou l’on ne peut pas se vacher au pieds des voies
le cas interessant ici est bien sur lorsque le + lourd grimpe
a vos calculettes
merci
Oui, il existe une méthode hautement scientifique pour calculer le poids maximum du grimpeur à assurer. Mais c’est un phénomène extrèmement complexe qui prend en compte des paramètres hautement précis. Un résultat mathématique, appelé théorème, est considéré comme tel lorsque le discours formel qui est censé convaincre de sa vérité suit une certaine structure rationnelle appelée démonstration, ou raisonnement déductif. Cette démonstration suit les lois de la logique.On nomme postulat un principe utilisé dans la construction d’un système déductif, mais qu’on ne démontre pas lui-même, sans pour autant s’interdire la possibilité de s’y essayer plus tard (en ce sens, le postulat se distingue de l’axiome, toujours posé au départ comme fondamental qu’on ne cherchera donc pas à démontrer). Il faut d’abord définir des postulats.On peut donc utiliser un postulat avec l’assentiment de l’auditeur, qui le prend comme un principe non démontré mais sans doute légitime, car semblant intuitivement non contestable (ou parce que prouvé ultérieurement par des démonstrations ne le faisant bien entendu pas intervenir (voir circularité ou tautologie). En épistémologie, un axiome est une vérité évidente en soi sur laquelle une autre connaissance peut se reposer, autrement dit peut être construite dessus. Précisons que tous les épistémologues n’admettent pas que les axiomes, dans ce sens du terme, existent. Dans certains courants philosophiques, comme l’objectivisme, le mot « axiome » a une connotation particulière. Un énoncé est axiomatique s’il est impossible de le nier sans se contredire. Exemple : « Il existe une vérité absolue » ou « Le langage existe » sont des axiomes.En mathématiques le mot axiome désignait une proposition qui est évidente en soi dans la tradition mathématique grecque, comme dans les Éléments d’Euclide. L’axiome est utilisé désormais, en logique mathématique, pour désigner une vérité première, à l’intérieur d’une théorie. L’ensemble des axiomes d’une théorie est appelé axiomatique. Cette axiomatique doit bien entendu être non-contradictoire ; c’est sa seule contrainte. Cette axiomatique définit la théorie ; ce qui signifie que l’axiome ne peut être remis en cause à l’intérieur de cette théorie, on dit alors que cette théorie est consistante. Un axiome représente donc plutôt un point de départ dans un système de logique et il peut être choisi arbitrairement. Bien entendu, la pertinence d’un théorie dépend de la pertinence de ses axiomes et de son interprétation. En réalité, c’est de la non cohérence de son interprétation, que vient la réfutation de la théorie non-contradictoire, et par voie de conséquence, de son axiomatique. L’axiome est donc à la logique mathématique, ce qu’est le postulat à la physique théorique. Des axiomes servent de base élémentaire pour tout système de logique formelle. Tout résultat que nous pouvons déduire des axiomes n’a pas besoin d’être un axiome. Toute affirmation qui ne peut être déduite des axiomes et dont la négation ne peut pas non plus se déduire de ces mêmes axiomes, peut raisonnablement être ajoutée comme axiome.
une démonstration est une déduction destinée à prouver la vérité de sa conclusion en s’appuyant sur des prémisses reconnues ou admises comme vraies ». La démonstration a deux points d’appui fondamentaux : celui de la logique et celui de la consistance du système dans lequel elle se déroule. A l’intérieur du système de la géométrie d’Euclide, on peut démontrer que la somme des trois angles d’un triangle forment 180°, équivalent à deux droits. On dresse pour cela des parallèles aux côtés du triangle, on examine les équivalences des angles alterne/internes et on démontre qu’effectivement la proposition « les trois angles du triangle font deux droits » est nécessairement vraie. Dans un système où les axiomes sont différents, par exemple dans la construction de la géométrie convexe de Riemann, cette propriété ne sera plus vraie, les trois angles font moins que 180°. Comme le triangle dessiné sur un ballon a des angles plus aigus. Une démonstration se déroule donc sur un plan beaucoup plus abstrait qu’une argumentation. Une démonstration est formelle. Elle ne sort pas du contexte du système logique dans laquelle elle prend place. Elle peut être correcte ou incorrecte, mais seulement par rapport aux règles d’inférence du système qui la soutient. Le professeur de mathématique fait très bien la différence entre une démonstration correcte et une démonstration incorrecte. Il maîtrise en effet les règles d’inférence du système. Dans la pratique, une démonstration prend dès lors souvent la forme d’un calcul, le calcul étant justement l’application d’une règle opératoire à l’intérieur d’un système. Pour ces différentes raisons, il est d’usage de rattacher l’usage rigoureux de la démonstration à la logique et aux mathématiques, tandis que l’on replacera l’argumentation dans l’ordre concret des faits, dans l’ordre de la vérité matérielle, les mathématiques demeurant sur le plan des idéalités, dans le champ de la vérité formelle. Parce que dans la démonstration la puissance de la logique se trouve libérée de toute entrave, de toute référence avec la nécessité de consulter des faits pour savoir si ce que l’on dit est vrai, la démonstration emporte avec elle une force que n’a jamais l’argumentation. La démonstration fournit des preuves contraignantes, l’argumentation, elle, ne fait que préciser les raisons en faveur ou contre une thèse déterminée. Dans la démonstration, l’esprit est obligé de plier, de s’incliner et il ne peut pas se dégager. Fondamentalement, nous ne pouvons pas nous dérober devant les conséquences de nos propres principes, parce qu’elles vont avec. Ce qui est agaçant, car cela vaut pour tous les principes, des axiomes mathématiques, aux principes de la logique, jusqu’aux principes des systèmes les plus dogmatiques… y compris ceux des sceptiques ! La vertu de la démonstration, telle que la déploie un professeur de mathématique en cours, c’est d’habituer l’élève à une rigueur qui l’oblige à suivre le fil de la logique, de ne plus procéder par association d’idées. La démonstration est un modèle d’objectivité (texte). La vertu de la démonstration est d’obliger l’esprit à s’émanciper de toute opinion ou vue trop subjective, au sens le plus vague du terme. La contrainte logique de la démonstration nous oblige à abandonner nos opinions personnelles, nos vues fantaisistes, pour nous soumettre à un système et à sa la logique. La démonstration est une école de formation intellectuelle en ce sens. Elle nous apprend l’impartialité. Elle nous oblige à reconnaître la vérité comme ce qui est indépendant de nos opinions personnelles, comme ce qui est valide pour tout esprit rationnel. Mais attention, cela doit s’entendre dans un sens qui n’est pas intuitif, car tout processus de démonstration est discursif, c’est-à-dire repose sur le raisonnement. La démonstration nous demande de nous situer d’emblée sur le terrain d’un auditoire universel, celui de la communauté des esprits capables de reconnaître la validité d’un savoir objectif. En pratique, cette communauté est celle du consensus des savants.
Le programme de l’approche objective de la connaissance de la science moderne a été d’emblée défini par le modèle de la démonstration mathématique. Le génie de Descartes et de Galilée est d’avoir mis en place une méthode dans laquelle l’univers est considéré comme un livre écrit en langage mathématique. C’est un programme très ambitieux, qui a conduit a des résultats immenses, mais qui sur le fond soulève une difficulté : est-il possible de soumettre la réalité dans son ensemble à un système unique et à l’arraisonnement de notre logique?
Pour résumer, je te donne ma méthode de calcul très vaguement simplifié.
1ère hyppothèse : Le grimpeur plus lourd que moi, est un con arrogant, alors je lui dis que si je l’assure, il risque de s’éclater au sol et qu’il serait donc plus prudent qu’il se trouve un assureur de son gabarit.
2ème hyppothèse : Le grimpeur plus lourd que moi est une personne hautement sympathique, alors je l’assure au grigri et je reste très vigilant, sachant que le seul risque est de décoller un peu du sol, situation très confortable pour le grimpeur qui se prend un vol dynamique.
Posté en tant qu’invité par Gepi:
J2MHV a écrit:
…
Pour résumer, je te donne ma méthode de calcul très vaguement
simplifié.
1ère hyppothèse : Le grimpeur plus lourd que moi, est un con
arrogant, …
Pourrais tu démontrer cette conjecture ???
Posté en tant qu’invité par J2MHV:
Gepi a écrit:
J2MHV a écrit:
…
Pour résumer, je te donne ma méthode de calcul très
vaguement
simplifié.
1ère hyppothèse : Le grimpeur plus lourd que moi, est un con
arrogant, …Pourrais tu démontrer cette conjecture ???
Très simple, Quand il se trouve - qu’après un travail mathématique rigoureux de démonstration - une conjecture est vraie, elle devient théorème et rejoint le royaume des faits mathématiques. Jusqu’à ce stade ultime de véracité, les mathématiciens doivent donc faire extrêmement attention lorsqu’ils font appel à une conjecture dans leurs structures logiques et leurs démonstrations. Par exemple, l’hypothèse de Riemann est une conjecture de la théorie des nombres qui énonce (entre autres choses) des prévisions sur la distribution des nombres premiers. Peu de théoriciens des nombres doutent du fait que l’hypothèse de Riemann soit vraie. Dans l’attente de sa preuve éventuelle, certains mathématiciens développent d’autres démonstrations qui reposent sur la vérité de cette conjecture. Cependant, ces « preuves » tomberaient en morceaux si cette hypothèse de Riemann se révélait fausse ou indécidable. Il y a donc un intérêt mathématique majeur à démontrer la vérité ou la fausseté des conjectures mathématiques pendantes.Bien que la plupart des conjectures les plus célèbres aient été vérifiées pour des kyrielles étonnantes de nombres, cela ne constitue pas une garantie contre un simple contre-exemple, qui réfuterait immédiatement la conjecture considérée. Par exemple, la conjecture de Syracuse - qui concerne l’arrêt d’une certaine suite de nombres entiers - a été examinée pour tous les nombres entiers jusqu’à 1,2 × 1012 (soit plus d’un million de millions). Cependant, elle a toujours le statut de conjecture car il peut toujours exister un contre-exemple de valeurs qui pourrait être trouvées au dela de 1,2 × 1012 et qui infirmeraient son énoncé. Toutes les conjectures ne finissent pas par être établies comme vraies ou fausses. Par exemple, l’hypothèse du continu - qui essaye d’établir la cardinalité relative de certains ensembles infinis - s’est avérée indécidable à partir de l’ensemble des axiomes généralement admis de la théorie des ensembles. Il est donc possible d’adopter cette assertion, ou sa négation, comme nouvel axiome de façon cohérente (comme nous pouvons également supposer le postulat de la parallèle d’Euclide comme vrai ou faux).En mathématiques, une assertion est une phrase mathématique, à laquelle il est possible, dans le cadre d’une théorie, d’attribuer une valeur de vérité vraie ou fausse, mais pas les deux (principe du tiers exclu). Autrement dit, nous devons pouvoir dire sans aucune ambiguïté si cette formulation est vraie ou fausse par rapport à un système d’axiomes donné et en concordance avec une logique mathématique. Un énoncé mathématique est dit indécidable dans un système axiomatique s’il est impossible de le déduire, ou de déduire sa négation, à partir des axiomes. Pour distinguer cette notion d’indécidabilité de la notion d’indécidabilité algorithmique (voir ci-dessous), on dit aussi que l’énoncé est indépendant du système d’axiomes. En termes plus concrets, cela veut dire qu’on demande au système de fournir une conclusion sans lui avoir fourni suffisamment d’hypothèses. Ainsi, l’âge du capitaine d’un bateau est indécidable en fonction du tonnage et de la vitesse du navire. En logique classique, d’après le théorème de complétude, une proposition est indécidable dans une théorie s’il existe des modèles de la théorie où la proposition est fausse et des modèles où elle est vraie. On utilise souvent des modèles, pour montrer qu’un énoncé est indépendant d’un système d’axiomes (dans ce cadre on préfère employer indépendant qu’indécidable). La propriété utilisée dans ce cas n’est pas le théorème de complétude mais sa réciproque, très immédiate, appelée parfois fidélité. Probablement est-ce là d’ailleurs la première apparition de la notion de modèle, avec la construction au XIXème siècle de modèles des géométries non classiques, ne vérifiant pas l’axiome des parallèles. Si l’on admet le fait assez intuitif que la géométrie euclidienne est cohérente – la négation de l’axiome des parallèles ne se déduit pas des autres axiomes – l’axiome des parallèles est bien alors indépendant des autres axiomes de la géométrie, ou encore indécidable dans le système formé des axiomes restant. Une théorie mathématique pour laquelle tout énoncé est décidable est dite complète, sinon elle est dite incomplète. Beaucoup de théories mathématiques sont naturellement incomplètes, parce qu’il y a évidemment des énoncés qui ne sont pas déterminés par les axiomes (théorie des groupes, des anneaux, …) . Certaines théories, comme la théorie des corps algébriquement clos sont complètes. Le théorème d’incomplétude de Gödel montre que toute théorie logique suffisamment puissante pour représenter l’arithmétique de Peano (l’arithmétique usuelle), est incomplète. Un problème de décision est dit décidable s’il existe un algorithme (ou une machine de Turing) qui le décide, sinon il est indécidable. Par exemple, le problème de l’arrêt est indécidable. En cas d’ambiguïté possible, on peut parler d’ indécidabilité algorithmique, pour distinguer cette notion de l’ indécidabilité logique exposée dans le paragraphe précédent. Dire qu’un problème est indécidable ne veut pas dire que les questions posées sont insolubles mais seulement qu’il n’existe pas de méthode unique et bien définie, applicable d’une façon mécanique, pour répondre à toutes les questions, en nombre infini, rassemblées dans un même problème. Un sous-ensemble des entiers naturels est dit décidable, quand le problème de l’appartenance d’un entier quelconque à cet ensemble est décidable, indécidable sinon. On généralise directement aux n-uplets d’entiers. On dit aussi d’un ensemble décidable qu’il est récursif. Le complémentaire d’un ensemble décidable est décidable. On montre en théorie de la calculabilité qu’un ensemble récursivement énumérable dont le complémentaire est récursivement énumérable est récursif (c’est à dire décidable). On généralise ces notions aux langages formels, par des codages à la Gödel. Il est possible aussi de les définir directement. Dans le cas ds théories logiques (closes donc par déduction), on parle donc de théorie décidable, ou de théorie indécidable. Ces notions ne doivent pas être confondues avec celles de théorie complète et théorie incomplète. Quand on parle d’une théorie décidable ou indécidable, c’est forcément de décidabilité algorithmique qu’il s’agit, jamais de décidabilité logique. Les deux notion de décidabilité interprètent chacune la notion intuitive de décision dans des sens clairement différents. Elles sont cependant liées. En effet, on considère en mathématiques qu’une démonstration, si elle peut être difficile à trouver, doit être « facile » à vérifier, en un sens très informel (et discutable, mais ce n’est pas l’objet de cet article). Quand on formalise, on traduit ceci en demandant que le problème de reconnaître si un assemblage de phrases est une démonstration formelle, est décidable. Pour que ceci soit exact, il faut supposer que l’ensemble des axiomes de la théorie est décidable, ce qui est très naturel. Sous cette hypothèse, l’ensemble des théorèmes d’une théorie devient récursivement énumérable, et donc une telle théorie, si elle est complète est alors décidable (voir article théorie axiomatique pour des justifications et détails supplémentaires). Le problème de l’arrêt. Dans ce cas, les questions portent sur tous les programmes informatiques (dans un langage suffisamment puissant, tel que tous ceux utilisés en pratique) et sur tous les états initiaux possibles de la mémoire (définis par une quantité finie d’information). Il s’agit de savoir si oui ou non un ordinateur s’arrêtera lorqu’il exécute un programme à partir de l’état initial de la mémoire. L’indécidabilité du problème de l’arrêt a été prouvée par Alan Turing. Plus généralement le théorème de Rice énoncée que toute question non triviale sur les programmes informatiques qui ne dépend que du résultat du calcul (terminer ou non, valeur calculée etc.) est indécidable. La question de savoir si oui ou non un énoncé de la logique du premier ordre est une loi logique (démontrable dans toute théorie), dépend de la signature du langage choisie (les symboles d’opération ou de relation …). Ce problème, parfois appelé problème de la décision, est indécidable pour le langage de l’arithmétique, et plus généralement pour n’importe quel langage égalitaire du premier ordre qui contient au moins un symbole de relation binaire (comme < ou ∈). Pour un langage égalitaire du premier ordre ne contenant que des symboles de prédicat unaires (calcul des prédicats égalitaire monadique), il est décidable. La question de savoir si oui ou non un énoncé du langage l’arithmétique (il faut les deux opérations, + et ×) est vraie dans le modèle standard de l’arithmétique est indécidable. La prouvabilité d’un énoncé à partir des axiomes de l’arithmétique de Peano est indécidable. Gödel a montré que cet ensemble est strictement inclus dans le précédent. Comme l’axiomatique de Peano as une infinité d’axiomes, cela ne se déduit pas de l’indécidabilité du problème de la décision dans le langage (voir ci-dessus). Les deux résultats se déduisent d’un résultat général pour les théories arithmétiques qui satisfont certaines conditions. L’arithmétique de Peano vérifie ces conditions, mais aussi l’arithmétique Q de Robinson, qui a un nombre fini d’axiomes. La prouvabilité d’un énoncé à partir des axiomes d’une théorie des ensembles cohérente, et plus généralement de toute théorie cohérente qui permet d’exprimer suffisamment riche d’arithmétique formelle est indécidable. La question de savoir si oui ou non une équation diophantienne a une solution. La preuve de son indécidabilité est le théorème de Matiyasevich (1970). La question de savoir si oui ou non une formule est une identité de la logique combinatoire, qui est une autre formulation du lambda-calcul. Son indécidabilité a été prouvée par Alonzo Church.
En conclusion, si le grimpeur plus lourd est un con arrogant, il a la grosse tête et les chevilles qui enflent, ce qui accroit encore le problême initial de la diiférence de poids entre assureur et assuré.
Posté en tant qu’invité par JPL:
Merci…bravo…j’aime
Juste une question, es tu aussi volubile quand tu grimpes (avant, pendant, après) avec ou sans apéro ?
Sur un site j’espère !
Posté en tant qu’invité par J.Marc:
Tiens, c’est marrant, quand on m’explique l’escalade à coups de théorèmes, je comprends beaucoup mieux !
Bon, ça n’engage que moi, mais il me semble que la très récente démonstration de la conjecture de Poincaré par le Russe Perelman permet de simplifier sensiblement ton argumentation.
En effet, il prouve en substance que nous sommes tous homéomorphes à des ballons, et comme tout le monde a pu en faire l’expérience, un ballon qui tombe rebondit sans se faire mal.
Posté en tant qu’invité par Pi2r:
J2MHV c’est la nouvelle mise à jour du module J2LH de réponse automatique pour forum dépeuplé?
Posté en tant qu’invité par osonsvosges:
Henri poincaré qui comme son frére Raymond, est originaire de Sampigny en Meuse pile poil entre deux sites d’escalade :
Lérouville
et
Saint Mihiel
[%sig%]
Posté en tant qu’invité par Gepi:
J.Marc a écrit:
Tiens, c’est marrant, quand on m’explique l’escalade à coups de
théorèmes, je comprends beaucoup mieux !
Bon, ça n’engage que moi, mais il me semble que la très récente
démonstration de la conjecture de Poincaré par le Russe
Perelman permet de simplifier sensiblement ton argumentation.
En effet, il prouve en substance que nous sommes tous
homéomorphes à des ballons, …
Tu es sûr de ça ?
Pour être homéomorphes à des ballons, ne devrais tu pas être exempt de trou ?
Ne serais tu pas plutôt homéomorphe à une bouée ;o))
Posté en tant qu’invité par J.Marc:
Gepi a écrit:
Pour être homéomorphes à des ballons, ne devrais tu pas être
exempt de trou ?
Ne serais tu pas plutôt homéomorphe à une bouée
Tu as entièrement raison, mais je n’ai pas voulu entrer dans les détails pour laisser le lecteur réfléchir un tantinet.
Evidemment, comme le stipule Poincaré, le grimpeur doit être simplement connexe, c’est-à-dire exempt de trou.
Le gros con, qui comme tout le monde le sait a la cervelle percée, n’est pas homéomorphe à un ballon, mais à une passoire.
Et une passoire rebondit très mal.
On rejoint ainsi les conclusion de J2MHV.
CQFD.
Posté en tant qu’invité par Gepi:
J.Marc a écrit:
Evidemment, comme le stipule Poincaré, le grimpeur doit être
simplement connexe,
« Connexe » oui c’est ça, j’ai eu un trou de mémoire, un seul, ça compte ?
Le gros con, qui comme tout le monde le sait a la cervelle
percée, n’est pas homéomorphe à un ballon, mais à une passoire.
Et une passoire rebondit très mal.
Peut-être, mais c’est pratique pour chopper les nouilles et donc à éviter en escalade.
On rejoint ainsi les conclusion de J2MHV.
J2MHV quoi ?
Posté en tant qu’invité par J.Marc:
Gepi a écrit:
Peut-être, mais c’est pratique pour chopper les nouilles et
donc à éviter en escalade.
Tu fais bien de le rappeler !
Posté en tant qu’invité par J.Marc:
Gepi a écrit:
PS : SVP que les taupins ou profs de physique ou de math ne me
tombent pas dessus
Je vais éviter, car vu mon poids, ça ne te ferait pas du bien.
PS : dois-je moi aussi prouver ma dernière assertion ?
Posté en tant qu’invité par jc:
Si je ne m’abuse, il doit mesurer dans les 1,8 x 1650763,73 fois la longueur d’onde dans le vide de la radiation correspondant à la transition entre les niveaux 2p10 et 5d5 de l’atome krypton 86. C’est un clone, donc.
Posté en tant qu’invité par Etienne:
J.Marc a écrit:
Gepi a écrit:
Peut-être, mais c’est pratique pour chopper les nouilles et
donc à éviter en escalade.Tu fais bien de le rappeler !
Et tu n’en profites pas pour nous faire un petit rappel sur la théorie des cordes ?
( avec autobloquant, le rappel, j’ai pas la journée…)
La page ne s’affiche pas ou plus, c’est dommage !
Il y avait quelle information ?